HyperCells#

In this tutorial we will see how the cell, model and supercell model graphs are constructed through the HyperCells package. These objects capture the tight-binding model specifications and can be used to conduct hyperbolic band theory analysis. Moreover, we go through the intended workflow and showcase which HyperCells objects need to be assembled in order to construct the cell, model and supercell model graphs through group theory in GAP.

Preliminaries#

To use the HyperCells package, start GAP and then load the package with:

gap> LoadPackage("HyperCells");

A typical workflow starts by setting up the (proper) triangle group, here we choose \(\Delta^{+}(2,8,8)\):

gap> tg := ProperTriangleGroup( [ 2, 8, 8 ] );
ProperTriangleGroup(2, 8, 8)

The returned object is of category ProperTriangleGroup. The presentation of the proper triangle group can be extracted by applying the operation FpGroup:

gap> FpGroup(tg);
<fp group on the generators [ x, y, z ]>

This represents a finitely presented group with rotation generators x, y, z and corresponding relators given by:

gap> GeneratorsOfGroup(FpGroup(tg));
[ x, y, z ]

gap> RelatorsOfFpGroup(FpGroup(tg));
[ x*y*z, x^2, y^8, z^8 ]

It is instructive to use the HyperBloch package in Mathematica in order to visualize how the fundamental Schwarz triangle s_f is transported in the \(\{8,8\}\)-tesselations of the hyperbolic plane when acting upon it with the rotation generators. However, we will restrain the exact details on how to obtain it for now, a detailed discussion can be found in the Flat-bands and Haldane model tutorials. The corresponding visualization in Poincaré disk looks as follows:

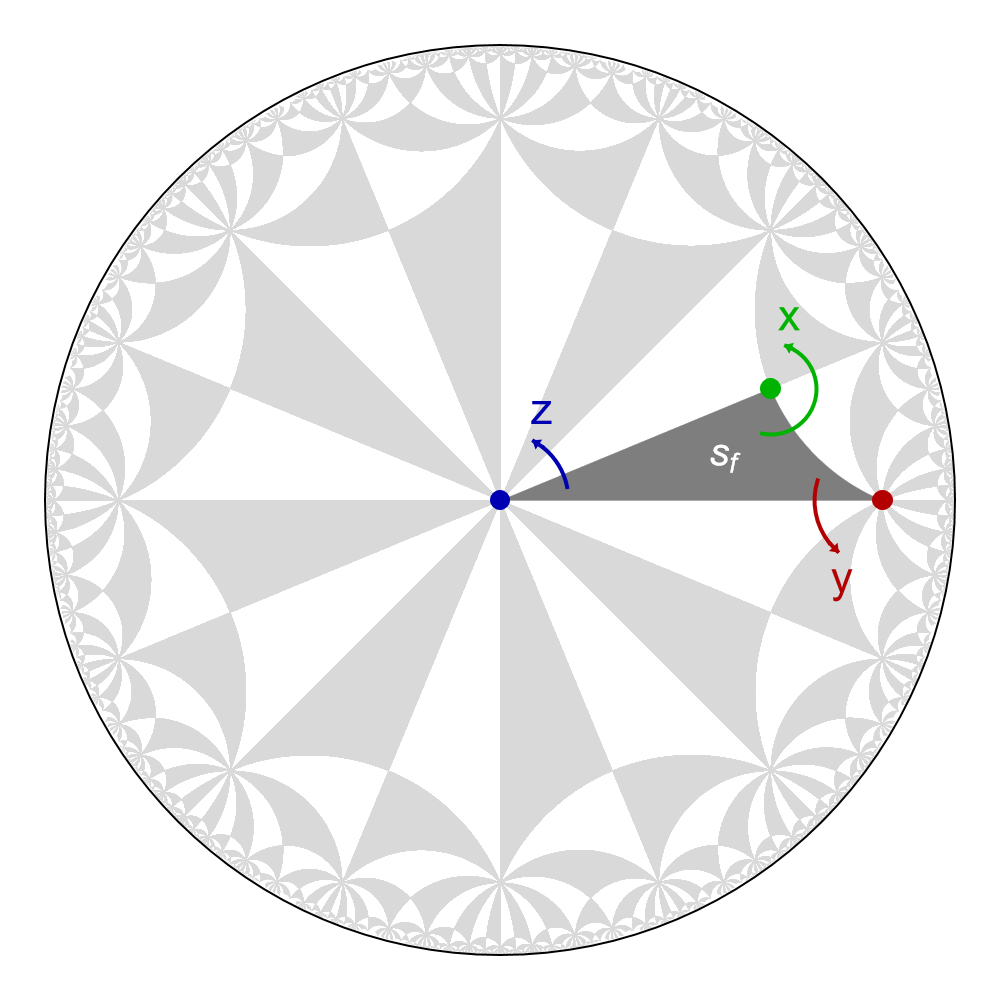
Next, we specify a unit cell of the lattice in terms of the quotient of the proper triangle group \(\Delta^{+}\) with a translation group \(\Gamma \triangleleft \Delta^{+}\). For that we can query the included database based on the work of Marston Conder, which allows us to select one of them:

gap> ListTGQuotients( [ 2, 8, 8 ] );
[ [ 2, 6 ], [ 3, 10 ], [ 3, 11 ], [ 5, 12 ], [ 5, 13 ], [ 9, 19 ], ... ]

In the following, we select the quotient denoted by T2.6, where the 2 indicates the genus of the surface on which the quotient group acts, and the 6 indicates the position in Conder’s list of all quotients with the same genus:

gap> q := TGQuotient( [ 2, 6 ] );
TGQuotient([ 2, 6 ], [ 2, 8, 8 ], 8, 2, Action reflexible [m,n], 
    [ x^2, x * y * z, x * z * y, y^3 * z^-1 ])

The returned object is of category TGQuotient. Alternatively, we can access the first entry appearing for \(\Delta^{+}(2,8,8)\) using:

gap> q := TGQuotient( 1, [ 2, 8, 8 ] );
TGQuotient([ 2, 6 ], [ 2, 8, 8 ], 8, 2, Action reflexible [m,n],
    [ x^2, x * y * z, x * z * y, y^3 * z^-1 ])

The TGQuotient object carries the defining information of the triangle group quotient, such as its order, the genus of the compactified unit cell it acts upon, the defining relators and other information, for example:

gap> TGQuotientOrder(q);
8

gap> TGQuotientGenus(q);
2

gap> TGQuotientRelators(q);
[ x^2, x * y * z, x * z * y, y^3 * z^-1 ]

Once we have the proper triangle group and the TGQuotient object, we can obtain the quotient group, which is isomorphic to the proper point group \(G^{+}\cong \Delta^{+}/\Gamma\):

gap> G := TGQuotientGroup( tg, q );
<fp group on the generators [ x, y, z ]>

or the associated translation group \(\Gamma\):

gap> TGTranslationGroup( tg, q );
TranslationGroup( < g1, g2, g3, g4 | g4*g3*g2*g1*g2^-1*g4^-1*g1^-1*g3^-1 > )

The number of generators in the translation group \(\Gamma\) is twice the genus of the compactified unit cell.

Cell graph#

The next step is to construct the graph representing the primitive cell. This graph corresponds to a triangular tessellation of the compactified cell and is stored as an object of category TGCellGraph. In addition to the triangle group and quotient, we also need to specify the vertex at which the cell should be centered (here we choose 3, corresponding to the z vertex of the fundamental Schwarz triangle):

gap> cg := TGCellGraph( tg, q, 3 : simplify := 5 );
TGCellGraph(
    TGCell( ProperTriangleGroup(2, 8, 8), [ x^2, x*y*z, x*z*y, y^3*z^-1 ] ),
    center = 3,
    vertices = [ [ 1, 1 ], [ 1, 2 ], [ 1, 3 ], [ 1, 4 ], [ 2, 1 ], [ 3, 1 ] ],
    edges = [ [ 1, 6, 1, <identity ...> ], ..., [ 6, 5, 8, g1^-1*g2*g3^-1 ] ],
    faces = [ [ [ 3, 1 ], [ 2, 1 ], [ 14, -1 ], [ 6, -1 ] ], ... ],
    boundary = [ [ <identity ...>, <identity ...>, 2, 1, 0, g1 ], ... ]
)

The option simplify specifies the maximum wordlength that should be checked for simplifying expressions in terms of the translation generators g1, g2, etc. The default value is 0 which means that no simplification is performed.

In tandem with the option simplify, another option simplifyMethod can be passed, which specifies whether to use the default brute force approach simplifyMethod=”BruteForce” or the Knuth-Bendix completion algorithm simplifyMethod=”KnuthBendix” for the simplification, provided the kbmag package is available.

While the cell graph itself represents the compactified unit cell, potential translations associated with the edges crossing from one copy of the cell to another are stored as well. The cell graph can be exported using the Export operation.

Model graph#

With the cell graph at hand, we can derive a model graph, such as a tessellation graph, i.e., the nearest-neighbor graph of the \(\{8,8\}\)-tesselation of the hyperbolic plane restricted to the primitive cell:

gap> model := TessellationModelGraph( cg, true : simplify := 0 );
TGCellModelGraph( 
    TGCell( ProperTriangleGroup(2, 8, 8), [ x^2, x*y*z, x*z*y, y^3*z^-1 ] ), 
    center = 3, 
    type = [ "TESS", [ 8, 8 ], [ "VEF", [ [ 3 ], [ 1 ], [ 2 ] ] ] ], 
    vertices = [ [ 3, 1 ] ], 
    edges = [[ 1, 1, [ 1, [ [ 1, 1 ], 1, 5 ] ], g1 ], [ 1, 1, [ 1, [ [ 1, 2 ], 4,  8 ] ], g4 ], 
        [ 1, 1, [ 1, [ [ 1, 3 ], 2, 6 ] ], g2 ], [ 1, 1, [ 1,  [ [ 1, 4 ], 3, 7 ] ], g3 ] ], 
    faces = [ [ [ 1, -1 ], [ 2, -1 ], [ 4, 1 ], [ 3, -1 ], [ 1, 1 ], [ 2, 1 ], 
        [ 4, -1 ], [ 3, 1 ] ] ] )

The result is an object of category TGCellModelGraph, which can be exported using the Export operation.

Supercell model graph#

Finally, the model graph defined on the primitive cell can be extended to a supercell, i.e., a cell specified by a translation subgroup \(\Gamma^{'}\triangleleft\Gamma\) of the original translation group \(\Gamma\). Here, we consider the one given by the quotient T3.11 (see tutorial Supercells for a in depth discussion) and first construct the symmetric cell, without simplifying the translation generators:

gap> sc := TGCellSymmetric( tg, TGQuotient( [ 3, 11 ] ), 3 );
TGCell( ProperTriangleGroup(2, 8, 8), [ x^2, x*y*z, x*z*y, y^-8 ] )

and then construct the supercell model graph:

gap> scmodel := TGSuperCellModelGraph( model, sc : simplify := 0 );
TGSuperCellModelGraph( 
    primitive cell = TGCell( ProperTriangleGroup(2, 8, 8), 
        [ x^2, x*y*z, x*z*y, y^3*z^-1 ] ), 
    supercell = TGCell( ProperTriangleGroup(2, 8, 8), 
        [ x^2, x*y*z, x*z*y, y^-8 ] ), 
    cell embedding = TGCellEmbedding( 
        primitive cell = TGCellTranslationGroup( < g1, g2, g3, g4 | 
            g2*g1^-1*g4^-1*g3*g2^-1*g1*g4*g3^-1 > ), 
        supercell = TGCellTranslationGroup( < g1, g2, g3, g4, g5, g6 | 
            g6*g4*g2*g1*g3*g5*g3^-1*g2^-1*g6^-1*g5^-1*g1^-1*g4^-1 > ), 
        transversal = [ <identity ...>, (x^-1*y^-1)^4*x^-1 ], 
        embedding = [ g1, g2, g3, g4, g5, g6 ] -> [ g1^-1*g4^-1, ... ] 
    ), 
    center = 3, 
    type = [ "TESS", [ 8, 8 ], [ "VEF", [ [ 3 ], [ 1 ], [ 2 ] ] ] ], 
    vertices = [ [ 3, 1, 1 ], [ 3, 1, 2 ] ], 
    edges = [ [ 1, 2, [ 1, 1, [ 1, [ [ 1, 1 ], 1, 5 ] ] ], <identity ...> ], ... ], 
    faces = [ ] 
)

which is returned as an object of category TGSuperCellModelGraph and can be exported using the Export operation. The vertices and edges of the supercell model graph retain information about the vertices and edges of the primitive cell model graph and the elements of the quotient group \(\Gamma_{pc}/\Gamma_{sc}\) distinguishing the different copies of the primitive cell in the supercell.