Coherent sequences#

The application of the supercell method relies on the construction of appropriate supercell sequences. These sequences, are associated with corresponding translation group sequences, and restricted to so-called coherent sequences of translation groups. In the previous tutorial Supercells we have seen how such sequences are constructed, but have kept their identification somewhat shrouded. As such, let us see how suitable supercell sequences can be determined.

In this tutorial we will look at two approaches to construct supercell sequences which consist of constructing a user defined function and a normal subgroup tree graph. A usual workflow starts by constructing the latter, which shows the normal subgroup relations between any given translation group extracted from quotient groups in Marston Conder’s list.

Introduction#

The supercell sequences used in the supercell method are constructed through quotients \(\Delta/\Gamma^{(m)}\) of the triangle groups \(\Delta\). Each triangle group quotient is associated with a corresponding translation group \(\Gamma^{(m)}\) which forms a normal subgroup of the triangle group \(\Delta\triangleright\Gamma^{(m)}\). The \(m\)’th consecutive supercell in the sequence, which we denote as the \(m\)-supercell, is thus associated with a corresponding translation group \(\Gamma^{(m)}\), which obeys the following normal subgroup relations:

(1)#\[\Delta\triangleright\Gamma^{(1)}\triangleright\Gamma^{(2)}\triangleright\cdot\cdot\cdot\triangleright\Gamma^{(m)}\triangleright\cdot\cdot\cdot\]

and \(\bigcap_{m\ge0}\Gamma^{(m)}=1\), where \(\Gamma^{(0)}=\Delta\).

Such sequences are called coherent sequences of translation groups, which enable us to accumulate higher dimensional irreducible representations of elements in the translation groups on the original primitive cell through the supercell method.

Preliminaries#

As usual, we start by constructing the proper triangle group, the quotient group for the primitive cell and additionally the corresponding translation group for the \(\{8,8\}\)-lattice in GAP:

# load the HyperCells package
LoadPackage( "HyperCells" );

# set up (proper) triangle group
tg := ProperTriangleGroup( [ 2, 8, 8 ] );

# specify the quotient defining the primitive cell
qpc := TGQuotient( 1, [ 2, 8, 8 ] );

# associated translation group
tgGamma_pc1 := TGTranslationGroup( tg, qpc );

# construct symmetric primitive cell
cgpc := TGCellGraph( tg, qpc, 3 : simplify := 5 );

# elementary nearest-neighbor model
model := TessellationModelGraph( cgpc, true : simplify := 5 );
Export( model, "{8,8}-tess_T2.6_3.hcm" ); # export

Skip to section Normal subgroup tree graph approach

On a first read, one may want to skip the section “Custom function approach” and resume at the section “Normal subgroup tree graph approach”.

Custom function approach#

Before constructing our custom function, let us go through the main points that should be considered in any user defined function that identifies coherent supercell sequences.

The \((m+1)\)-supercell in a coherent supercell sequence is associated with a translation group \(\Gamma^{(m+1)}\), which is a consecutive normal subgroup of the translation group \(\Gamma^{(m)}\) (of the \(m\)-supercell) and the proper triangle group \(\Delta^{+}\). We extract the translation groups \(\Gamma^{(m)}\) from quotient groups in Marston Conder’s list. Since they are normal subgroups of \(\Delta^{+}\), it is sufficient to check if the set of elements in a translation group \(\Gamma^{(m+1)}\) forms a subset of \(\Gamma^{(m)}\).

For example, let us extract the translation group associated with the second quotient group in order to identify the first candidate for the \(2\)-supercell:

q2 := TGQuotient(2, [2, 8, 8]);
tgGamma_2 := TGTranslationGroup(tg, q2);

This translation group, however, is not a normal subgroup of the previous translation group:

gap> IsSubset(AsTGSubgroup(tgGamma_pc1), AsTGSubgroup(tgGamma_2));
false

but the next one is:

q3 := TGQuotient(3, [2, 8, 8]);
tgGamma_3 := TGTranslationGroup(tg, q3);

and:

gap> IsSubset(AsTGSubgroup(tgGamma_pc1), AsTGSubgroup(tgGamma_3));
true

Next, we impose that supercells are symmetric aggregates of primitive cells. Thus, restricting the selection of quotient groups to those with point groups \(G^{(m)}\) and proper point groups \(G^{+ (m)}\) with order \(|G^{(m)}| = 2|G^{+ (m)}|\).

The extracted quotient groups are isomorphic to the proper point groups \(G^{+ (m)}\). For example, the third quotient group, isomorphic to the proper point group \(G^{+ (2)}\), is:

Gplus := TGQuotientGroup(tg, q3);

The point groups \(G^{(m)}\) can be constructed through the (full) triangle group \(\Delta\) by using the embedding of the proper triangle group \(\Delta^{+}\) in the (full) triangle group \(\Delta\):

# presentation of the (full) triangle group
DELTA := FpGroup(TriangleGroup(Signature(tg)));
a := DELTA.1;; b := DELTA.2;; c := DELTA.3;

# embedding homomorphism of D in DELTA
embDDELTA := GroupHomomorphismByImagesNC(D, DELTA, GeneratorsOfGroup(D), [a*b, b*c, c*a]);

We can use this homomorphism in order to find the relators of \(G^{+ (m)}\) in terms of generators of \(\Delta\), and thus enabling us to construct \(G^{(m)}\). For example, for the third quotient we find \(G^{(2)}\):

# relators of the proper point group
rels := TGQuotientRelators(tg, q3);

# point group
relsfull := List(rels, r -> Image(embDDELTA, r));
G := DELTA / relsfull;

We can check if our constraint is fulfilled:

gap> Order(G) = 2 * Order(Gplus);
true

As such, a possible function to retrieve a particular supercell sequence is given:

getMthSupercellQuotient := function(tg, tgGamma, n1)
        local tgGamma_n, Gamma1, qn, signat, switch, 
        i, D, rels, G, Gplus, a, b, c, DELTA, 
        embDDELTA, relsfull;

  # signature (2, q, p)
  signat := Signature(tg);

  # presentation of the proper triangle group  
  D := FpGroup(tg);

  # translation group in terms of generators x, y, z
  Gamma1 := AsTGSubgroup(tgGamma);
	
  # presentation of the (full) triangle group
  DELTA := FpGroup(TriangleGroup(Signature(tg)));
  a := DELTA.1;; b := DELTA.2;; c := DELTA.3;

  # embedding homomorphism of D in DELTA
  embDDELTA := GroupHomomorphismByImagesNC(D, DELTA,
      GeneratorsOfGroup(D), [a*b, b*c, c*a]);

  i := n1;
  switch := false;
  while switch = false do
                
    qn := TGQuotient(i, signat);
    tgGamma_n := TGTranslationGroup(tg, qn);
    switch := IsSubset(Gamma1, AsTGSubgroup(tgGamma_n));
    if switch then
    
      # proper point group
      Gplus := D / rels;

      # relators of the proper point group
      rels := TGQuotientRelators(tg, qn);
      
      # (full) point group
      relsfull := List(rels, r -> Image(embDDELTA, r));
      G := DELTA / relsfull;
      
      # ensure that quotient is mirror symmetric
      if not Order(G) = 2 * Order(Gplus) then
        switch := false;
      fi; 
     fi;
  
   i := i + 1;
  od;

 return [qn, tgGamma_n, i];
end;;

This function takes as arguments a ProperTriangleGroup and a TGTranslationGroup. The integer n1 is the first index of the quotient groups in the list ListTGQuotients( [ 2, 8, 8 ] ) that will be checked to satisfy the conditions stated above. Let us apply this function in order to retrieve a first supercell:

qANDtgGamma_sc1 := getMthSupercellQuotient(tg, tgGamma_pc1, 2);

The first supercell in this sequence is given by:

gap> qsc_3_11 := qANDtgGamma_sc1[1];;
gap> TGQuotientName(qsc_3_11);
[ 3, 11 ]

The TGQuotientName returns the label given in M. Conder’s list, where 3 is the genus of the Riemann surface the quotient acts upon and 11 the index in the list. Let us retrieve the next 5 supercells, together with the corresponding tessellation graphs, i.e., the nearest-neighbor graphs of the \(\{8,8\}\)-tesselation of the hyperbolic plane by iterating over the list of available quotient:

n0 := 2;
tgGamma_sc_i := tgGamma_pc1;

for i in [1 .. 6] do

  # find appropriate quotient group
  qANDtgGamma_sc_i := getMthSupercellQuotient(tg, tgGamma_sc_i, n0);
  qsc_i := qANDtgGamma_sc_i[1];;
  tgGamma_sc_i := qANDtgGamma_sc_i[2];; 
  n0 := qANDtgGamma_sc_i[3];;

  # construct tessellation graphs
  sc_i := TGCellSymmetric(tg, qsc_i, 3);
  scmodel_i := TGSuperCellModelGraph(model, sc_i);

  # export file
  sc_i_index := TGQuotientName(qsc_i);
  sc_i_label := StringFormatted("-tess_T2.6_3_sc-T{}.{}.hcs", sc_i_index[1], sc_i_index[2]);
  scmodel_i_name := JoinStringsWithSeparator(["{8,8}", sc_i_label], "");
  Export(scmodel_i,  scmodel_i_name);

od;

Download GAP Code

The sequence of quotient groups we were able to extract is:

T2.6, T3.11, T5.13, T9.20, T17.29, T33.44 and T65.78

This coincides with the supercell sequence 1 we have considered in the tutorial Supercells.

Normal subgroup tree graph approach#

Identifying sequences of supercells through user defined functions might be cumbersome. The built-in function to identify normal subgroup relations of the translation groups provides efficient access to all sequences which are normal subgroups of \(\Delta^{+}\) and obey the normal subgroup relation \(\Delta^{+}\triangleright \Gamma^{(1)} \triangleright \Gamma^{(2)} \triangleright \cdot \cdot \cdot \triangleright \Gamma^{(m)} \triangleright \cdot \cdot \cdot\) available through the access of Marston Conder’s list. It can be used to build advanced user defined functions as well as to visualize appropriate sequences in tree graphs we denote as normal subgroup tree graphs.

In order to visualize a normal subgroup tree graph we first need to construct an adjacency matrix, which describes the normal subgroup relations between any pairwise distinct translation groups of a \(\{p,q\}\)-tesselation of the hyperbolic plane. Since these matrices are in general sparse we may choose a corresponding representation. The adjacency matrix for the \(\{8,8\}\)-tesselation, with quotient groups acting upon Riemann surfaces up to genus 66, can be extracted as follows (caution, this may take a few minutes):

tgQSS := TGQuotientSequencesStructure(tg : sparse := true, boundByGenus := 66);;

The returned object is of category TGQuotientSequencesStructure. This enables us to extract one of the longest coherent supercell sequence available, with supercells that can be symmetrically aggregated with primitive cells:

gap> LongestSequence(tgQSS);
[ [ 2, 6 ], [ 3, 11 ], [ 5, 13 ], [ 9, 20 ], [ 17, 29 ], [ 33, 44 ], [ 65, 78 ] ]

which, once again, correspond to the supercell sequence 1 we have considered in the tutorial Supercells. We can also specify the starting quotient of the sequence:

gap> LongestSequence(tgQSS : quotient := [ 9, 23 ]);
[ [ 9, 23 ], [ 17, 30 ], [ 33, 46 ], [ 65, 78 ] ]

Next, let us export the adjacency matrix in order to visualize the normal subgroup tree graph in Mathematica, which can be done by using the Export operation:

Export(tgQSS, "(2,8,8)-QSS-BBG_66_sparse.hcqs");

Download generated files Download GAP Code

The adjacency matrix can be imported analogously to cell, model and supercell model graphs. The Import function is used to read the file, while the ImportQuotientSequencesStructureString function is used to parse the string and construct the adjacency matrix:

(* Preliminaries *)
<< PatrickMLenggenhager`HyperBloch`
SetDirectory[NotebookDirectory[]];

(* Import quotient sequences structure *)
QSS = ImportQuotientSequencesStructureString[Import["(2,8,8)-QSS-BBG_66_sparse.hcqs"]];

Normal subgroup tree graphs can be visualized with the high-level visualization function VisualizeQuotientSequences. It is convenient to first consider a subgraph with genera of compactified unit cells up to genus \(30\), which provides an overseeable example. We can achieve this by passing a function to the option VertexFilter, which takes quotient names Tg.n of the form {g, n} as arguments and returns a boolean:

VisualizeQuotientSequences[QSS,
  EdgeArrowSize -> 0.01, ImageSize -> 1100, 
  VertexFilter -> (#[[1]] < 30 &),
  VertexLabelStyle -> Directive[Black, Italic, 15] ]

Every vertex corresponds to a translation group \(\Gamma^{(m)}\) associated with a corresponding unit cell and denoted with the label of the triangle group quotient \(\Delta^{+}/\Gamma^{(m)}\), with quotients in the tabulated list of quotients by Marston Conder. Each \(\Gamma^{(m)}\) is a normal subgroup of \(\Delta\). Vertices highlighted in red indicate that the corresponding unit cell can be assembled mirror symmetrically with Schwarz triangles. Black vertices do not admit a mirror-symmetric unit cell, which limits some of the functionality of HyperCells package for them, namely those functions that construct or rely on symmetric cells (but not those working with generic supercells). Pairwise distinct vertices \(\Gamma^{(m)}\), \(\Gamma^{(m+1)}\) connected by a directed edge obey the normal subgroup relation \(\Gamma^{(m)} \triangleright \Gamma^{(m+1)}\).

Let us visualize the entire normal subgroup tree graph. We choose to emphasize the vertices associated with compactified unit cells of lower genera. This can be achieved by passing a function to the option LayerDistributionFunction, which distributes the layers of distinct genera in a desired way. In addition, we try to avoid overlapping vertex labels by placing the labels alternately above and below the vertices of the tree graph through the option VertexLabelPlacement:

fullGraph = VisualizeQuotientSequences[QSS,
 EdgeArrowSize -> 0.01, ImageSize -> 1140, 
 LayerDistributionFunction -> (6.5 Log[#] &),
 VertexLabelPlacement -> "Alternate"]

Let us highlight the supercell sequence 1 we have previously determined in GAP. This can be achieved with the option VertexFilter and HighlightSubgraph set to True:

keepVertices = {{2, 6}, {3, 11}, {5, 13}, {9, 20}, {17, 29}, {33, 44}, {65, 78}};

VisualizeQuotientSequences[QSS,
 EdgeArrowSize -> 0.01, EdgeStyle -> Directive[Darker[Blue, 0.25], Thick, Opacity[0.2]], 
 HighlightSubgraph -> True, ImageSize -> 1140, LayerDistributionFunction -> (6.5 Log[#] &),
 VertexFilter -> (MemberQ[keepVertices, #] &), VertexLabelPlacement -> "Alternate"]

SubgroupTreegraph {8,8}-lattice BBG 66 scSQ 1

We can determine coherent sequences through the built-in Mathematica functions, such as FindPath or the resource function FindLongetPath, etc.. Let us reconstruct the sequences we have considered in the Supercells tutorial (where we adopt the sequence labels introduced in said tutorial).

The initial and the final vertex in the supercell sequence 1 are:

initialVertex = {2, 6};
finalVertex = {65, 78};

FindPath can be used to determine all sequences that connect the initial with the final vertex. The last sequence corresponds to the sequence we have previously considered:

sq1Lst = FindPath[fullGraph, initialVertex, finalVertex, Infinity, All];

sq1 = sq1Lst[[-1]]

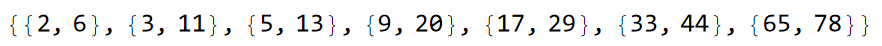
We can find the supercell sequences 1A and 2A analogously. The supercell sequence 1A can be found as follows:

initialVertex = {3, 10}; finalVertex = {65, 81};
sq1ALst = FindPath[fullGraph, initialVertex, finalVertex, Infinity, All];
sq1A = sq1Lst[[1]]

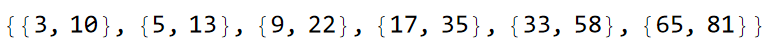
and the supercell sequence 2A:

initialVertex = {5, 12}; finalVertex = {65, 79};
sq2ALst = FindPath[fullGraph, initialVertex, finalVertex, Infinity, All];
sq2A = sq1Lst[[2]]

Download Mathematica Notebook

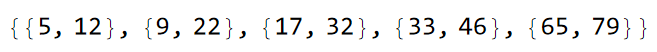
Highlighting multiple coherent sequences (bonus)#

We can use the VisualizeQuotientSequences function to highlight multiple coherent sequences in the full normal subgroup tree graph. In order to avoid the inclusion of superfluous edges, we can use the option EdgeFilter instead of VertexFilter. The corresponding edges are easily constructed:

sequnceLst = {sq1, sq1A, sq2A};
edgeLst =  Table[
  DirectedEdge[sequnceLst[[i, j]], sequnceLst[[i, j + 1]]], 
  {i, 3}, {j, Length[sequnceLst[[i]][[2 ;;]]]}];
allEdges = Flatten[edgeLst, 1];

Let us highlight the three sequences by specifying three color maps:

cfunc = (ColorData["SunsetColors", "ColorFunction"] /@ (1 - Range[3]/3));
colorTables = Flatten[Table[
  Style[edgeLst[[i, j]], Directive[cfunc[[i]], AbsoluteThickness[4]], Opacity[1]],
    {i, 3}, {j, Length@edgeLst[[i]]}], 1];

Therefore:

VisualizeQuotientSequences[QSS,
  EdgeArrowSize -> 0.01, EdgeFilter -> (MemberQ[allEdges, #] &), 
  EdgeStyle -> Directive[Darker[Blue, 0.25], Thick, Opacity[0.2]], 
  HighlightSubgraph -> True, HighlightSubgraphEdgeStyle -> colorTables, 
  ImageSize -> 1140, LayerDistributionFunction -> (6.5 Log[#] &), 
  VertexSize -> 0.5, VertexLabelPlacement -> "Alternate"]